29.11.2020. Кој што сака веднаш да ги види резултатите од симулацијата за месец декември, нека прескокне веднаш на точка II.
I. Често добивам злонамерни, омаловажувачки и навредливи коментари на разни портали, дека како инженер не требало да се мешам во медицински и епидемиолошки работи. Поради тоа решив да ја разјаснам оваа дилема, кој што знае и со што треба да се занимава.
Најпрво, проучувањето на динамиката на епидемијата има малку заедничко со медицината, која најмногу се занимава со познавањето на човековото тело, разните физиолошки и патолошки процеси, дијагностицирањето и лекувањето на болестите. Најсоодветната научна дисциплина се нарекува ДИНАМИКА НА ПРОЦЕСИ. Но што е точно динамика на процеси?
Заради проектирање и водење на разни системи, обично (но не исклучиво) во рамките на производните процеси, многу важно е да се знае како се однесува процесот (во нашиот случај епидемијата) и менувањето на одредени карактеристични големини (броеви на нови случаи, активни, хоспитализирани, оздравени и починати).
Како основа за прикажување на однесувањето на системот служи математичкиот опис. Математичкиот опис на било кој систем го чинат множество од разни математички изрази, таблици и дијаграми кои квантитативно ги опишуваат врските меѓу карактеристичните големини на системот. Често таквиот опис се нарекува математички модел или само модел.
Моделот може да биде статички и динамички. Статичкиот не мора нужно да прикажува само мирување, туку и стационарен режим на работа, како моменталното рамномерно ширење на заразувањето при ефективен репродукционен број Rt=1.
За нас сепак најважен е динамичкиот модел, кој го опишува однесувањето на системот (епидемијата), при што карактеристичните големини се променливи со текот на времето.
Поради тоа динамичкиот модел се претставува со една или повеќе обични или парцијални диференцијални равенки, во кои што се појавуваат разни изводи (деривации) на карактеристичните големини. Тие ги претставуваат разните брзини и забрзувања на карактеристичните големини со текот на времето.
Токму со истражување и проучување на временските промени на карактеристичните големини на системот и опишувањето на основните закони на неговото однесување се занимава посебната научно-техничка дисциплина – динамиката на процеси.
Динамиката на процеси, според потребниот математички апарат за изучување, е речиси 90% слична со една друга, сродна дисциплина, системи за автоматско управување (САУ).
За да се овладее добро со динамиката на процеси, покрај математиката потребно е знаење од областа на теоретската механика, термодинамиката и хидрауликата (кај машинците), односно теоријата на електрични кола (кај електро инженерите).
Со тие предзнаења и многу вежбање, односно пракса, инженерот е во состојба да постави математички модел на системот (системи диференцијални или дури интегро-диференцијални равенки), кои потоа се анализираат и решаваат со методите на динамиката на процеси, односно автоматското управување.
Кога сме кај епидемијата како систем, таа најдобро се опишува со систем од три или четири диференцијални равенки, кои ја опишуваат динамиката на растот на бројот на нови случаи, равенка на континуитетот на активните случаи, затворањето на случаите со оздравување и уми-рање, динамиката на бројот на хоспитализираните случаи и вкупните случаи.
За да можеме да поставиме добар модел, најпрво мораме да се запознаеме со самиот феномен на епидемијата, разните временски константи на доцнење од контактот до заразувањето, временскиот интервал од заразување до оздравување и умирање.
Секако, многу е важен феноменот на стекнување на привремен имунитет после прележување на болеста и времетраењето на истиот, што моментално е најголемата непозната во моделот.
Сосема накратко да кажеме дека доколку времетраењето на стекнатиот имунитет е барем два пати подолго од времето од избувнувањето до пикот, тогаш е можно целосно згаснување на епидемијата (што не значи дека не може повторно да избувне откако ќе се изгуби имунитетот).
Во спротивно, епидемијата преминува во ендемска болест која се усталува во стационарен режим после определено време.
Моментално работам токму на таков модел, којшто го зема предвид ограниченото времетраење на стекнатиот имунитет и ендемското одржување на заразувањето.
Како што гледаме, епидемијата како процес е многу повеќе техника отколку медицина, иако од медицината, односно поточно вирусологијата и епидемиологијата, користиме некои многу важни временски константи.
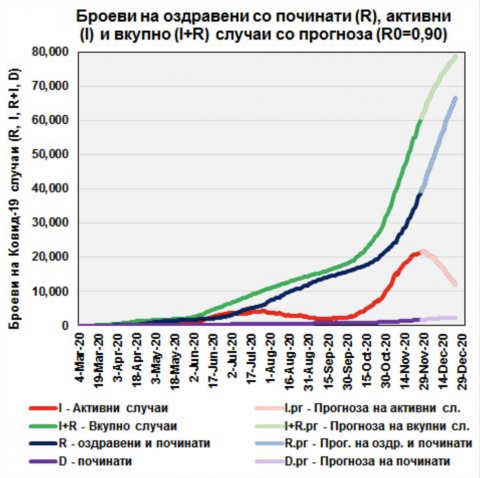
II. А сега, да видиме практична примена на динамиката на процесите преку моделирање на динамиката на епидемијата и предвидување на идните вкупни броеви на дијагностицирани, активни и оздравени случаи, како и поч-инати (на првиот дијаграм).
Кога ВФ вели дека мерките се соодветно дозирани и дека бројките наскоро ќе започнат да опаѓаат, треба да го прашате за колку ќе опаднат, да речеме, бројките на поч-инати до Нова година. Нормално дека не знае, ниту може да знае, затоа што му недостига математичко-техничко знаење, моделирање на динамиката на епидемискиот процес и решавање на тие равенки.
Но затоа има некој што го знае сето тоа и што е најважно, знаењето го споделува бесплатно.
За таа цел ќе направиме една симулација во едно крајно оптимистичко сценарио (како да е според ВФ), дека ефективниот репродукционен број од последната вредност Rt=0,96 ќе продолжи да се намалува и дека во текот на целиот месец декември ќе има просечна вредност Rt=0,90. Исто така, ќе претпоставиме дека сегашната стапка на леталитет (CFR) од 2,8% прилично ќе се намали, па нејзината средна вредност во текот на цел месец декември ќе изнесува само 2,5%.
Со овие преоптимистички прeтпоставки на првиот дијаграм гледаме како би се менувале вкупниот број на случаи, активните и оздравените со текот на времето. Решенијата, добиени со интегрирање на диференцијалните равенки на епидемијата, со почетни услови земени на ден 28.11.2020, се прикажани со криви линии со бледи бои.
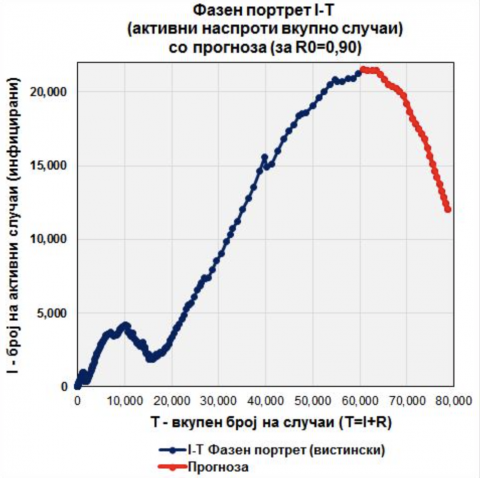
Според ова многу оптимистичко сценарио, бројот на активни, а со нив и хоспитализирани речиси би се преполовил (црвената линија на првиот и вториот дијаграм).
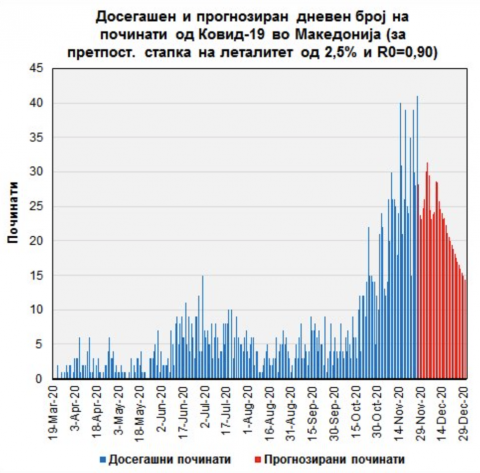
Што се однесува до дневниот број на поч-инатите, оптимистичката проекција е прикажана со црвена боја на третиот дијаграм. При тоа, најдобро е прикажаните вредности да се сметаат за средни вредности, околу кои би имало дневни флуктуации.
Како што гледаме, заради доцнењето од две недели во однос на намалувањето на бројот на нови случаи, бројот на починати нема толку бргу да опаѓа.
Конечно, на четвртата слика гледаме како би се менувал вкупниот број на починати во текот на декември, дури и при едно вакво многу оптимистичко сценарио.
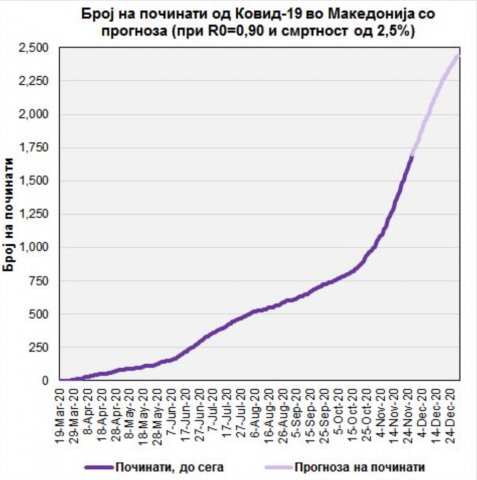
Забележуваме дека првите две недели бледо виолетовата линија би искачувала речиси еднакво стрмо како досега, за да при крајот на месецот подзабави.
Ете, тоа е цената на одолговлекувањето со мерките и чекањето бројките да опаднат по природен пат. Ако 2300-2500 вкупно починати на крајот од декември не им изгледа многу, само нека продолжат вака. Таман да стигнеме до светската топ-5 листа според морталитетот на милион жители.
Во наредните десетина дена ќе видиме дали навистина Rt ќе може да се намали до 0,9 и таму да се задржи или сите прогнози ќе бидат корегирани на полошо.






Comments are closed for this post.